6 Types de données¶

6.1 Typage¶

Inhérent au fonctionnement interne de l'ordinateur, un langage de programmation s'abstrait plus ou moins du mode de stockage interne des données telles qu'elles sont enregistrées dans la mémoire. De la même manière que dans la vie réelle, il n'est pas possible de rendre de la monnaie à un vendeur à moins d'un cinquième de centime près, il n'est pas possible pour un ordinateur de stocker des informations numériques avec une précision infinie.

Aussi, les langages de programmation sont dits typés lorsqu'ils confient au programmeur la responsabilité de choisir comment une information sera stockée en mémoire, et non typés lorsque ce choix est implicite. Chacun des langages à ses avantages et ses inconvénients et pour reprendre l'exemple du rendu de monnaie, il serait ennuyant d'autoriser d'enregistrer des informations financières avec une précision meilleure qu'une pièce de cinq centimes, car il serait alors impossible à un caissier de rendre la monnaie correctement. Dans cette situation on préférera les langages typés et heureusement C est un langage fortement typé.

Les types de données ne se bornent pas qu'aux informations numériques, il existe des types plus complexes qui permettent par exemple de traiter des caractères tels que A ou B. Ce chapitre à pour objectif de familiariser le lecteur aux différents types de données disponibles en C.

Note

Standard ISO

Les ingénieurs sont friands des standards et qui plus est lorsqu'ils sont internationaux. Ainsi afin d'éviter le crash malheureux d'une fusée causé par la mésentente de deux ingénieurs de différents pays, il existe la norme ISO 80000-2 qui définit précisément ce qu'est un entier, s'il doit inclure ou non le zéro, que sont les nombres réels, etc. Bien entendu les compilateurs, s'ils sont bien faits, cherchent à respecter au mieux ces normes internationales, et vous ?

6.2 Stockage et interprétation¶

Rappelez-vous qu'un ordinateur ne peut stocker l'information que sous forme binaire et qu'il n'est à même de manipuler ces informations que par paquets de bytes. Aussi un ordinateur 64-bits manipulera avec aisance des paquets de 64-bits, mais plus difficilement des paquets de 32-bits. Ajoutons qu'il existe encore des microcontrôleurs 8-bits utilisés dans des dispositifs à faible consommation et qui peinent à manipuler des types de plus grande taille. Stocker une température avec une trop grande précision et effectuer des opérations mathématiques sur toute la précision serait une erreur, car le microcontrôleur n'est simplement pas adapté à manipuler ce type d'information.

Considérons le paquet de 32-bit suivant, êtes-vous à même d'en donner une signification?

01000000 01001001 00001111 11011011

Il pourrait s'agir :

de 4 caractères de 8-bits :
- 01000000 @
- 01001001 I
- 00001111 \x0f
- 11011011 Û
ou de 4 nombres de 8-bits: 64, 73, 15, 219,
ou de deux nombres de 16-bits 18752 et 56079,
ou alors un seul nombre de 32-bit 3675212096.
Peut-être est-ce le nombre -40331460896358400.000000 lu en little endian,
ou encore 3.141592 lu en big endian.

Qu'en pensez-vous ?

Lorsque l'on souhaite programmer à bas niveau, vous voyez que la notion de type de donnée est essentielle, car en dehors d'une interprétation subjective: "c'est forcément PI la bonne réponse", rien ne permet à l'ordinateur d'interpréter convenablement l'information enregistrée en mémoire.

Le typage permet de résoudre toute ambiguïté.

int main() {
    union {
        uint8_t u8[4];
        uint16_t u16[2];
        uint32_t u32;
        float f32;
    } u = { 0b01000000, 0b01001001, 0b00001111, 0b11011011 };

    printf("'%c', '%c', '%c', '%c'\n", u.u8[0], u.u8[1], u.u8[2], u.u8[3]);
    printf("%hhu, %hhu, %hhu, %hhu\n", u.u8[0], u.u8[1], u.u8[2], u.u8[3]);
    printf("%hu, %hu\n", u.u16[0], u.u16[1]);
    printf("%u\n", u.u32);
    printf("%f\n", u.f32);
    u.u32 = (
        ((u.u32 >> 24) & 0xff) | // move byte 3 to byte 0
        ((u.u32 << 8) & 0xff0000) | // move byte 1 to byte 2
        ((u.u32 >> 8) & 0xff00) | // move byte 2 to byte 1
        ((u.u32 << 24) & 0xff000000) // byte 0 to byte 3
    );
    printf("%f\n", u.f32);
}

6.3 Boutisme¶

La hantise de l'ingénieur bas-niveau c'est le boutisme aussi appelé endianess. Ce terme étrange a été popularisé par l'informaticien Dany Cohen en référence aux Voyages de Gulliver de Jonathan Swift. Dans ce conte les habitants de Lilliput refusent d'obéir à un décret obligeant à manger les œufs à la coque par le petit bout (petit boutisme/little endian), la répression incite les rebelles à manger leurs œufs par le gros bout (gros boutisme/big endian).

Aujourd'hui encore, il existe des microprocesseurs qui fonctionnent en big endian alors que d'autres sont en little endian. C'est à dire que si une information est stockée en mémoire comme suit :

[0x40, 0x49, 0xf, 0xdb]

Faut-il la lire de gauche à droite ou de droite à gauche? Cela vous paraît trivial, mais si cet exemple était mentionné dans un livre rédigé en arabe, quelle serait alors votre réponse ?

Imaginons qu'un programme exécuté sur un microcontrôleur big-endian 8-bit envoie par Bluetooth la valeur 1'111'704'645, qui correspond au nombre de photons ayant frappé un détecteur optique. Il transmet donc les 4 octets suivants: 0x42, 0x43, 0x44, 0x45. L'ordinateur qui reçoit les informations décode 1'162'101'570. Les deux ordinateurs n'interprètent pas les données de la même façon, et c'est un problème que la plupart des ingénieurs électroniciens rencontrent un jour dans leur carrière.

6.4 Les nombres entiers¶

Les nombres entiers sont des nombres sans virgule et incluant le zéro. Ils peuvent donc être négatifs, nuls ou positifs. Mathématiquement ils appartiennent à l'ensemble des entiers relatifs.

Comme aucun ordinateur ne dispose d'un espace de stockage infini, ces nombres excluent les infinis positifs et négatifs, et sont donc bornés, cela va de soi.

6.4.1 Les entiers naturels¶

En mathématiques, un entier naturel est un nombre positif ou nul. Chaque nombre à un successeur unique et peut s'écrire avec une suite finie de chiffres en notation décimale positionnelle, et donc sans signe et sans virgule. L'ensemble des entiers naturels est défini de la façon suivante :

\[\mathbb{N} = {0, 1, 2, 3, ...}\]

En informatique, ces nombres sont par conséquent non signés, et peuvent prendre des valeurs comprises entre \(0\) et \(2^N-1\) où \(N\) correspond au nombre de bits avec lesquels la valeur numérique sera stockée en mémoire. Il faut naturellement que l'ordinateur sur lequel s'exécute le programme soit capable de supporter le nombre de bits demandé par le programmeur.

En C, on nomme ce type de donnée unsigned int, int étant le dénominatif du latin integer signifiant "entier".

Voici quelques exemples des valeurs minimales et maximales possibles selon le nombre de bits utilisés pour coder l'information numérique :

Tableau 6.1 Stockage d'un entier non signé sur différentes profondeurs¶
Profondeur	Minimum	Maximum
8 bits	0	255 (\(2^8 - 1\))
16 bits	0	65'535 (\(2^{16} - 1\))
32 bits	0	4'294'967'295 (\(2^{32} - 1\))
64 bits	0	18'446'744'073'709'551'616 (\(2^{64} - 1\))

Notez l'importance du \(-1\) dans la définition du maximum, car la valeur minimum \(0\) fait partie de l'information même si elle représente une quantité nulle. Il y a donc 256 valeurs possibles pour un nombre entier non signé 8-bits, bien que la valeur maximale ne soit que de 255.

6.4.2 Les entiers relatifs¶

Mathématiquement un entier relatif appartient à l'ensemble \(\mathbb{Z}\):

\[\mathbb{Z} = {..., -3, -2, -1, 0, 1, 2, 3, ...}\]

Les entiers relatifs sont des nombres signés et donc ils peuvent être négatifs, nuls ou positifs et peuvent prendre des valeurs comprises entre \(-2^{N-1}\) et \(+2^{N-1}-1\) où \(N\) correspond au nombre de bits avec lesquels la valeur numérique sera stockée en mémoire. Notez l'asymétrie entre la borne positive et négative.

En C on dit que ces nombres sont signed. Il est par conséquent correct d'écrire signed int bien que le préfixe signed soit optionnel, car le standard définit qu'un entier est par défaut signé. La raison à cela relève plus du lourd historique de C qu'à des préceptes logiques et rationnels.

Voici quelques exemples de valeurs minimales et maximales selon le nombre de bits utilisés pour coder l'information :

Tableau 6.2 Stockage d'un entier signé sur différentes profondeurs¶
Profondeur	Minimum	Maximum
8 bits	-128	+127
16 bits	-32'768	+32'767
32 bits	-2'147'483'648	+2'147'483'647

En mémoire ces nombres sont stockés en utilisant le complément à deux qui fait l'objet d'une section à part entière.

6.4.3 Les entiers bornés¶

Comme nous l'avons vu, les degrés de liberté pour définir un entier sont :

Signé ou non signé
Nombre de bits avec lesquels l'information est stockée en mémoire

À l'origine le standard C restait flou quant au nombre de bits utilisés pour chacun des types et aucune réelle cohérence n'existait pour la construction d'un type. Le modificateur signed était optionnel, le préfixe long ne pouvait s'appliquer qu'au type int et long et la confusion entre long (préfixe) et long (type) restait possible. En fait, la plupart des développeurs s'y perdaient et s'y perd toujours ce qui menait à des problèmes de compatibilités des programmes entre eux.

6.4.3.1 Types standards¶

La construction d'un type entier C est la suivante :

Ce qu'il faut retenir c'est que chaque type de donnée offre une profondeur d'au moins \(N\) bits, ce qui est l'information minimale essentielle pour le programmeur. La liste des types de données standards en C pour les entiers est donnée au Tableau 6.3.

Tableau 6.3 Types entiers standards¶
Type	Signe	Profondeur	Format
`char`	?	`CHAR_BIT`	`%c`
`signed char`	signed	au moins 8 bits	`%c`
`unsigned char`	unsigned	au moins 8 bits	`%c`
`short` `short int` `signed short` `signed short int`	signed	au moins 16 bits	`%hi`
`unsigned short` `unsigned short int`	unsigned	au moins 16 bits	`%hu`
`unsigned` `unsigned int`	unsigned	au moins 32 bits	`%u`
`int` `signed` `signed int`	signed	au moins 32 bits	`%d`
`unsigned` `unsigned int`	unsigned	au moins 32 bits	`%u`
`long` `long int` `signed long` `signed long int`	signed	au moins 32 bits	`%li`
`unsigned long` `unsigned long int`	unsigned	au moins 32 bits	`%lu`
`long long` `long long int` `signed long long` `signed long long int`	signed	au moins 64 bits	`%lli`
`unsigned long long` `unsigned long long int`	unsigned	au moins 64 bits	`%llu`

Avec l'avènement de C99, une meilleure cohésion des types a été proposée dans le fichier d'en-tête stdint.h. Cette bibliothèque standard offre les types suivants :

Fig. 6.1 Flux de construction d'un entier standardisé¶

6.4.3.2 Types réformés¶

Voici les types standards qu'il est recommandé d'utiliser lorsque le nombre de bits de l'entier doit être maîtrisé.

Tableau 6.4 Entiers standard défini par `stdint`¶
Type	Signe	Profondeur	Format
`uint8_t`	unsigned	8 bits	`%c`
`int8_t`	signed	8 bits	`%c`
`uint16_t`	unsigned	16 bits	`%hu`
`int16_t`	signed	16 bits	`%hi`
`uint32_t`	unsigned	32 bits	`%u`
`int32_t`	signed	32 bits	`%d`
`uint64_t`	unsigned	64 bits	`%llu`
`int64_t`	signed	64 bits	`%lli`

À ces types s'ajoutent les types rapides (fast) et minimums (least). Un type nommé uint_least32_t garanti l'utilisation du type de donnée utilisant le moins de mémoire et garantissant une profondeur d'au minimum 32 bits. Il est strictement équivalent à unsigned int.

Les types rapides, moins utilisés vont automatiquement choisir le type adapté le plus rapide à l'exécution. Par exemple si l'architecture matérielle permet un calcul natif sur 48-bits, elle sera privilégiée par rapport au type 32-bits.

Exercice 6.1¶

Donnez la valeur des expressions ci-dessous :

+ 10 + 7 – 3
/ 2
+ 5 / 2
(24 + 5) / 2
/ 5 / 2
/ (5 / 2)
% 5 – 5
/ 5 – 5
% 3
-8 % 3
% -3
-8 % -3

Exercice 6.2¶

Quel sera le contenu de j après l'exécution de l'instruction suivante :

uint16_t j = 1024 * 64;

6.4.3.3 Modèle de donnée¶

Comme nous l'avons évoqué plus haut, la taille des entiers short, int, ... n'est pas précisément définie par le standard. On sait qu'un int contient au moins 16-bits, mais il peut, selon l'architecture, et aussi le modèle de donnée, prendre n'importe quelle valeur supérieure. Ceci pose des problèmes de portabilité possibles si le développeur n'est pas suffisamment consciencieux et qu'il ne s'appuie pas sur une batterie de tests automatisés.

Admettons que ce développeur sans scrupule développe un programme complexe sur sa machine de guerre 64-bits en utilisant un int comme valeur de comptage allant au-delà de dix milliards. Après tests, son programme fonctionne sur sa machine, ainsi que celle de son collègue. Mais lorsqu'il livre le programme à son client, le processus crash. En effet, la taille du int sur l'ordinateur du client est de 32-bits. Comment peut-on s'affranchir de ce type de problème?

La première solution est de toujours utiliser les types proposés par <stdint.h> lorsque la taille du type nécessaire est supérieure à la valeur garantie. L'autre solution est de se fier au modèle de données :

Tableau 6.5 Modèle de données¶
Modèle de donnée	`short`	`int`	`long`	`long long`	`size_t`	Système d'exploitation
LP32	16	16	32		32	Windows 16-bits, Apple Macintosh (très vieux)
ILP32	16	32	32	64	32	Windows x86, Linux/Unix 32-bits
LLP64	16	32	32	64	64	Microsoft Windows x86-64, MinGW
LP64	16	32	64	64	64	Unix, Linux, macOS, Cygwin
ILP64	16	64	64	64	64	HAL (SPARC)
SILP64	64	64	64	64	64	UNICOS (Super ordinateur)

6.5 Les nombres réels¶

Mathématiquement, les nombres réels \(\mathbb{R}\), sont des nombres qui peuvent être représentés par une partie entière, et une liste finie ou infinie de décimales. En informatique, stocker une liste infinie de décimale demanderait une quantité infinie de mémoire et donc, la précision arithmétique est contrainte.

Au début de l'ère des ordinateurs, il n'était possible de stocker que des nombres entiers, mais le besoin de pouvoir stocker des nombres réels s'est rapidement fait sentir. La transition s'est faite progressivement, d'abord par l'apparition de la virgule fixe, puis par la virgule flottante.

Le premier ordinateur avec une capacité de calcul en virgule flottante date de 1942 (ni vous ni moi n'étions probablement né) avec le Zuse's Z4, du nom de son inventeur Konrad Zuse.

6.5.1 Virgule fixe¶

Prenons l'exemple d'un nombre entier exprimé sur 8-bits, on peut admettre facilement que bien qu'il s'agisse d'un nombre entier, une virgule pourrait être ajoutée au bit zéro sans en modifier sa signification.

┌─┬─┬─┬─┬─┬─┬─┬─┐
│0│1│0│1│0│0│1│1│ = 2^6 + 2^4 + 2^1 + 2^0 = 64 + 16 + 2 + 1 = 83
└─┴─┴─┴─┴─┴─┴─┴─┘
                , / 2^0     ----> 83 / 1 = 83

Imaginons à présent que nous déplacions cette virgule virtuelle de trois éléments sur la gauche. En admettant que deux ingénieurs se mettent d'accord pour considérer ce nombre 0b01010011 avec une virgule fixe positionnée au quatrième bit, l'interprétation de cette grandeur serait alors la valeur entière divisée par 8 (\(2^3\)). On parvient alors à exprimer une grandeur réelle comportant une partie décimale :

┌─┬─┬─┬─┬─┬─┬─┬─┐
│0│1│0│1│0│0│1│1│ = 2^6 + 2^4 + 2^1 + 2^0 = 64 + 16 + 2 + 1 = 83
└─┴─┴─┴─┴─┴─┴─┴─┘
          ,       / 2^3     ----> 83 / 8 = 10.375

Cependant, il manque une information. Un ordinateur, sans yeux et sans bon sens, est incapable sans information additionnelle d'interpréter correctement la position de la virgule puisque sa position n'est encodée nulle part. Et puisque la position de cette virgule est dans l'intervalle [0..7], il serait possible d'utiliser trois bits supplémentaires à cette fin :

┌─┬─┬─┬─┬─┬─┬─┬─┐
│0│1│0│1│0│0│1│1│ = 2^6 + 2^4 + 2^1 + 2^0 = 64 + 16 + 2 + 1 = 83
└─┴─┴─┴─┴─┴─┴─┴─┘
          ┌─┬─┬─┐
          │0│1│1│ / 2^3     ----> 83 / 8 = 10.375
          └─┴─┴─┘

Cette solution est élégante, mais demande à présent 11-bits contre 8-bits initialement. Un ordinateur n'étant doué que pour manipuler des paquets de bits souvent supérieurs à 8, il faudrait ici soit étendre inutilement le nombre de bits utilisés pour la position de la virgule à 8, soit tenter d'intégrer cette information, dans les 8-bits initiaux.

6.5.2 Virgule flottante¶

Imaginons alors que l'on sacrifie 3 bits sur les 8 pour encoder l'information de la position de la virgule. Appelons l'espace réservé pour positionner la virgule l' exposant et le reste de l'information la mantisse, qui en mathématique représente la partie décimale d'un logarithme (à ne pas confondre avec la mantis shrimp, une quille ou crevette mante boxeuse aux couleurs particulièrement chatoyantes).

  exp.  mantisse
┞─┬─┬─╀─┬─┬─┬─┬─┦
│0│1│0│1│0│0│1│1│ = 2^4 + 2^1 + 2^0 = 16 + 2 + 1 = 19
└─┴─┴─┴─┴─┴─┴─┴─┘
   └────────────> / 2^1 ----> 19 / 2 = 9.5

Notre construction nous permet toujours d'exprimer des grandeurs réelles, mais avec ce sacrifice, il n'est maintenant plus possible d'exprimer que les grandeurs comprises entre \(1\cdot2^{7}=0.0078125\) et \(63\). Ce problème peut être aisément résolu en augmentant la profondeur mémoire à 16 ou 32-bits. Ajoutons par ailleurs que cette solution n'est pas à même d'exprimer des grandeurs négatives.

Dernière itération, choisissons d'étendre notre espace de stockage à ,4 octets. Réservons un bit de signe pour exprimer les grandeurs négatives, 8 bits pour l'exposant et 23 bits pour la mantisse :

 ┌ Signe 1 bit
 │        ┌ Exposant 8 bits
 │        │                             ┌ Mantisse 23 bits
 ┴ ───────┴──────── ────────────────────┴──────────────────────────
┞─╀─┬─┬─┬─┬─┬─┬─┐┌─╀─┬─┬─┬─┬─┬─┬─┐┌─┬─┬─┬─┬─┬─┬─┬─┐┌─┬─┬─┬─┬─┬─┬─┬─┦
│0│0│0│1│0│0│0│0││0│1│0│0│1│0│0│0││1│1│0│1│1│1│1│1││0│1│0│0│0│0│0│1│
└─┴─┴─┴─┴─┴─┴─┴─┘└─┴─┴─┴─┴─┴─┴─┴─┘└─┴─┴─┴─┴─┴─┴─┴─┘└─┴─┴─┴─┴─┴─┴─┴─┘

Peu à peu, nous nous rapprochons du Standard for Floating-Point Arithmetic (IEEE 754). La formule de base est la suivante :

\[x = s\cdot b^e\sum_{k=1}^p f_k\cdot b^{-k},\; e_{\text{min}} \le e \le e_{\text{max}}\]

Avec :

\(s\): Signe (\(\pm1\))
\(b\): Base de l'exposant, un entier \(>1\).
\(e\): Exposant, un entier entre \(e_\text{min}\) et \(e_\text{max}\)
\(p\): Précision, nombre de digits en base \(b\) de la mantisse
\(f_k\): Entier non négatif plus petit que la base \(b\).

Étant donné que les ordinateurs sont plus à l'aise à la manipulation d'entrées binaire, la base est 2 et la norme IEEE nomme ces nombres binary16, binary32 ou binary64, selon le nombre de bits utilisé pour coder l'information. Les termes de Single precision ou Double precision sont aussi couramment utilisées.

Les formats supporté par un ordinateur ou qu'un microcontrôleur équipé d'une unité de calcul en virgule flottante (FPU pour Floating point unit) sont les suivants :

IEEE-754	Exposant	Mantisse	Signe
`binary32`	8 bits	23 bits	1 bit
`binary64`	11 bits	52 bits	1 bit

Prenons le temps de faire quelques observations.

Une valeur encodée en virgule flottante sera toujours une approximation d'une grandeur réelle.
La précision est d'autant plus grande que le nombre de bits de la mantisse est grand.
La base ayant été fixée à 2, il est possible d'exprimer \(1/1024\) sans erreur de précision, mais pas \(1/1000\).
Un ordinateur qui n'est pas équipé d'une FPU sera beaucoup plus lent (10 à 100x) pour faire des calculs en virgule flottante.
Bien que le standard C99 définisse les types virgule flottante float, double et long double, ils ne définissent pas la précision avec laquelle ces nombres sont exprimés, car cela dépend de l'architecture du processeur utilisé.

6.5.3 Simple précision¶

Le type float aussi dit à précision simple utilise un espace de stockage de 32-bits organisé en 1 bit de signe, 8 bits pour l'exposant et 23 bits pour la mantisse. Les valeurs pouvant être exprimées sont de :

\(\pm\inf\) lorsque l'exposant vaut 0xff
\((-1)^{\text{sign}}\cdot2^{\text{exp} - 127}\cdot1.\text{significand}\)
\(0\) lorsque la mantisse vaut 0x00000

La valeur de 1.0 est encodée :

\[\begin{split}0\:01111111\:00000000000000000000000_2 &= \text{3f80}\: \text{0000}_{16} \\ &= (-1)^0 \cdot 2^{127-127} \cdot \frac{(2^{23} + 0)}{2^{23}} \\ &= 2^{0} \cdot 1.0 = 1.0\\\end{split}\]

La valeur maximale exprimable :

\[\begin{split}0\:11111110\:11111111111111111111111_2 &= \text{7f7f}\: \text{ffff}_{16} \\ &= (-1)^0 \cdot 2^{254-127} \cdot \frac{(2^{23} + 838'607)}{2^{23}} \\ &≈ 2^{127} \cdot 1.9999998807 \\ &≈ 3.4028234664 \cdot 10^{38}\end{split}\]

La valeur de \(-\pi\) (pi) est :

\[\begin{split}1\:10000000\:10010010000111111011011_2 &= \text{4049}\: \text{0fdb}_{16} \\ &= (-1)^1 \cdot 2^{128-127} \cdot \frac{(2^{23} + 4'788'187)}{2^{23}} \\ &≈ -1 \cdot 2^{1} \cdot 1.5707963 \\ &≈ -3.14159274101\end{split}\]

Vient s'ajouter les valeurs particulières suivantes :

00000000 00000000000000000000000₂ ≡ 0000 0000₁₆ ≡ 0
11111111 00000000000000000000000₂ ≡ 7f80 0000₁₆ ≡ inf
11111111 00000000000000000000000₂ ≡ ff80 0000₁₆ ≡ −inf

6.5.4 Double précision¶

La double précision est similaire à la simple précision, mais avec une mantisse à 52 bits et 11 bits d'exposants.

Exercice 6.3¶

Donnez la valeur des expressions ci-dessous :

+ 10. + 7. – 3.
/ 2.
+ 5. / 2.
/ 5. / 2.
/ (5. / 2.)
* 13. % 7.
3E30 + 1.

6.6 Les caractères¶

Les caractères, ceux que vous voyez dans cet ouvrage, sont généralement représentés par des grandeurs exprimées sur 1 octet (8-bits):

97 ≡ 0b1100001 ≡ 'a'

Historiquement, alors que les informations dans un ordinateur ne sont que des 1 et des 0, il a fallu établir une correspondance entre une grandeur binaire et le caractère associé. Un standard a été proposé en 1963 par l'ASA, l'American Standards Association aujourd'hui ANSI qui ne définissait alors que 63 caractères imprimables et comme la mémoire était en son temps très cher, un caractère n'était codé que sur 7 bits.

Fig. 6.2 Table ASCII ASA X3.4 établie en 1963¶

Aujourd'hui la table ASCII de base définit 128 caractères qui n'incluent pas les caractères accentués.

Fig. 6.3 Table ANSI INCITS 4-1986 (standard actuel)¶

Chaque pays et chaque langue utilise ses propres caractères et il a fallu trouver un moyen de satisfaire tout le monde. Il a été alors convenu d'encoder les caractères sur 8-bits au lieu de 7 et de profiter des 128 nouvelles positions pour ajouter les caractères manquants tels que les caractères accentués, le signe euro, la livre sterling et d'autres. Le standard ISO/IEC 8859 aussi appelé standard Latin définit 16 tables d'extension selon les besoins des pays. Les plus courantes en Europe occidentale sont les tables ISO-8859-1 ou (latin1) et ISO-8859-15 (latin9):

Fig. 6.4 Table d'extension ISO-8859-1 (haut) et ISO-8859-15 (bas)¶

Ce standard a généré durant des décennies de grandes frustrations et de profondes incompréhensions chez les développeurs, et utilisateurs d'ordinateur. Ne vous est-il jamais arrivé d'ouvrir un fichier texte et de ne plus voir les accents convenablement ? C'est un problème typique d'encodage.

Pour tenter de remédier à ce standard incompatible entre les pays Microsoft à proposé un standard nommé Windows-1252 s'inspirant de ISO-8859-1. En voulant rassembler en proposant un standard plus général, Microsoft n'a contribué qu'à proposer un standard supplémentaire venant s'inscrire dans une liste déjà trop longue. Et l'histoire n'est pas terminée...

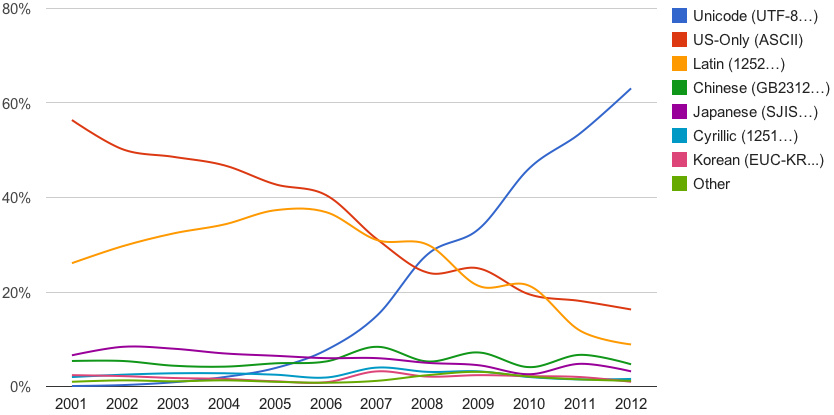
Avec l'arrivée d'internet et les échanges entre les Arabes (عَرَب‎), les Coréens (한국어), les Chinois avec le chinois simplifié (官话) et le chinois traditionnel (官話), les Japonais qui possèdent deux alphabets ainsi que des caractères chinois (日本語), sans oublier l'ourdou (پاکِستان) pakistanais et tous ceux que l'on ne mentionnera pas, il a fallu bien plus que 256 caractères et quelques tables de correspondance. Ce présent ouvrage, ne pourrait d'ailleurs par être écrit sans avoir pu résoudre, au préalable, ces problèmes d'encodage; la preuve étant, vous parvenez à voir ces caractères qui ne vous sont pas familiers.

Un consensus planétaire a été atteint en 2008 avec l'adoption majoritaire du standard Unicode (Universal Coded Character Set) plus précisément nommé UTF-8.

Fig. 6.5 Tendances sur l'encodage des pages web en faveur de UTF-8 dès 2008 (src)¶

L'UTF-8 est capable d'encoder 11'112'064 caractères en utilisant de 1 à 4 octets. Ken Thompson, dont nous avons déjà parlé en introduction est à l'origine de ce standard. Par exemple le devanagari caractère ह utilisé en Sanskrit possède la dénomination unicode U+0939 et s'encode sur 3 octets: 0xE0 0xA4 0xB9

En programmation C, un caractère char ne peut exprimer sans ambigüité que les 128 caractères de la table ASCII standard et selon les conventions locales, les 128 caractères d'extension.

Voici par exemple comment déclarer une variable contenant le caractère dollar :

char c = '$';

Attention donc au caractère '3' qui correspond à la grandeur hexadécimale 0x33:

#include <stdio.h>

int main(void) {
    char c = '3';
    printf("Le caractère %c vaut 0x%x en hexadécimal ou %d en décimal.\n", c, c, c);
    return 0;
}

6.7 Chaîne de caractères¶

Une chaîne de caractères est simplement la suite contiguë de plusieurs caractères dans une zone mémoire donnée. Afin de savoir lorsque cette chaîne se termine, le standard impose que le dernier caractère d'une chaîne soit NUL ou \0.

La chaîne de caractère Hello sera en mémoire stockée en utilisant les codes ASCII suivants.

char string[] = "Hello";

  H   E   L   L   O  \0
┌───┬───┬───┬───┬───┬───┐
│ 72│101│108│108│111│ 0 │
└───┴───┴───┴───┴───┴───┘

 0x00 01001000
 0x01 01100101
 0x02 01101100
 0x03 01101100
 0x04 01101111
 0x05 00000000

Exercice 6.4¶

Indiquez si les constantes littérales suivantes sont valides ou invalides.

'a'
'A'
'ab'
'\x41'
'\041'
'\0x41'
'\n'
'\w'
'\t'
'\xp2'
"abcdef"
"\abc\ndef"
"\'\"\\"
"Hello \world !\n"

Exercice 6.5¶

Pour les instructions ci-dessous, indiquer quel est l'affichage obtenu.

char a = 'a';
short sh1 = 5;
float f1 = 7.0f;
int i1 = 7, i2 = 'a';

printf("Next char: %c.\n", a + 1);
printf("Char: %3c.\n", a);
printf("Char: %-3c.\n", a);
printf("Chars: \n-%c.\n-%c.\n", a, 'z' - 1);
printf("Sum: %i\n", i1 + i2 - a);
printf("Taux d’erreur\t%i %%\n", i1);
printf("Quel charabia horrible:\\\a\a\a%g\b\a%%\a\\\n", f1);
printf("Inventaire: %i4 pieces\n", i1);
printf("Inventory: %i %s\n", i1, "pieces");
printf("Inventaire: %4i pieces\n", i1);
printf("Inventaire: %-4i pieces\n", i1);
printf("Mixed sum: %f\n", sh1 + i1 + f1);
printf("Tension: %5.2f mV\n", f1);
printf("Tension: %5.2e mV\n", f1);
printf("Code: %X\n", 12);
printf("Code: %x\n", 12);
printf("Code: %o\n", 12);
printf("Value: %i\n", -1);
printf("Value: %hi\n", 65535u);
printf("Value: %hu\n", -1);

6.8 Les booléens¶

Un booléen est un type de donnée à deux états consensuellement nommés vrai (true) et faux (false) et destiné à représenter les états en logique booléenne (Nom venant de George Boole fondateur de l'algèbre éponyme).

La convention est d'utiliser 1 pour mémoriser un état vrai, et 0 pour un état faux, c'est d'ailleurs de cette manière que les booléens sont encodés en C.

Les booléens ont étés introduits formellement en C avec C99 et nécessitent l'inclusion du fichier d'en-tête stdbool.h. Avant cela le type boolean était _Bool et définir les états vrais et faux était à la charge du développeur.

#include <stdbool.h>

bool is_enabled = false;
bool has_tail = true;

Afin de faciliter la lecture du code, il est courant de préfixer les variables booléennes avec les préfixes is_ ou has_.

À titre d'exemple, si l'on souhaite stocker le genre d'un individu (mâle, ou femelle), on pourrait utiliser la variable is_male.

6.9 Énumérations¶

Ce style d'écriture permet de définir un type de données contenant un nombre fini de valeurs. Ces valeurs sont nommées textuellement et définies numériquement dans le type énuméré.

enum ColorCode {
    COLOR_BLACK, // Vaut zéro par défaut
    COLOR_BROWN,
    COLOR_RED,
    COLOR_ORANGE,
    COLOR_YELLOW,
    COLOR_GREEN,
    COLOR_BLUE,
    COLOR_PURPLE,
    COLOR_GRAY,
    COLOR_WHITE
};

Le type d'une énumération est apparenté à un entier int. Sans autre précisions, la première valeur vaut 0, la suivante 1, etc.

Il est possible de forcer les valeurs de la manière suivante :

typedef enum country_codes {
    CODE_SWITZERLAND=41,
    CODE_FRANCE=33,
    CODE_US=1
} CountryCodes;

ou encore :

typedef enum country_codes {
    CODE_SWITZERLAND=41,
    CODE_BELGIUM=32
    CODE_FRANCE, // Sera 33...
    CODE_SPAIN, // Sera 34...
    CODE_US=1
} CountryCodes;

Pour ne pas confondre un type énuméré avec une variable, on utilise souvent la convention d'une notation en capitales. Pour éviter d’éventuelles collisions avec d'autres types, un préfixe est souvent ajouté.

L'utilisation d'un type énuméré peut être la suivante :

void call(enum country_codes code) {
    switch(code) {
    case CODE_SWITZERLAND :
        printf("Calling Switzerland, please wait...\n");
        break;
    case CODE_BELGIUM :
        printf("Calling Belgium, please wait...\n");
        break;
    case CODE_FRANCE :
        printf("Calling France, please wait...\n");
        break;
    default :
        printf("No calls to this country are allowed yet!\n");
    }
}

6.10 Type incomplet¶

Un type incomplet est un qualificatif de type de donnée décrivant un objet dont sa taille en mémoire n'est pas connue.

6.11 Type vide (void)¶

Le type void est particulier. Il s'agit d'un type dit incomplet, car la taille de l'objet qu'il représente en mémoire n'est pas connue. Il est utilisé comme type de retour pour les fonctions qui ne retournent rien :

void shout() {
    printf("Hey!\n");
}

Il peut être également utilisé comme type générique comme la fonction de copie mémoire memcpy

void *memcpy(void * restrict dest, const void * restrict src, size_t n);

Le mot clé void ne peut être utilisé que dans les contextes suivants :

Comme paramètre unique d'une fonction, indiquant que cette fonction n'a pas de paramètres int main(void)
Comme type de retour pour une fonction indiquant que cette fonction ne retourne rien void display(char c)
Comme pointeur dont le type de destination n'est pas spécifié void* ptr

6.12 Promotion implicite¶

Généralement le type int est de la même largeur que le bus mémoire de donnée d'un ordinateur. C'est-à-dire que c'est souvent, le type le plus optimisé pour véhiculer de l'information au sein du processeur. Les registres du processeur, autrement dit ses casiers mémoires, sont au moins assez grand pour contenir un int.

Aussi, la plupart des types de taille inférieure à int sont automatiquement et implicitement promus en int. Le résultat de a + b lorsque a et b sont des char sera automatiquement un int.

char	\(\Rightarrow\)	int
short	\(\Rightarrow\)	int
int	\(\Rightarrow\)	long
long	\(\Rightarrow\)	float
float	\(\Rightarrow\)	double

Notez qu'il n'y a pas de promotion numérique vers le type short. On passe directement à un type int.

Exercice 6.6¶

Soit les instructions suivantes :

int n = 10;
int p = 7;
float x = 2.5;

Donnez le type et la valeur des expressions suivantes :

x + n % p
x + p / n
(x + p) / n
.5 * n
.5 * (float)n
(int).5 * n
(n + 1) / n
(n + 1.0) / n

Exercice 6.7¶

Représentez les promotions numériques qui surviennent lors de l'évaluation des expressions ci-dessous :

char c;
short sh;
int i;
float f;
double d;

c * sh - f / i + d;
c * (sh – f) / i + d;
c * sh - f - i + d;
c + sh * f / i + d;

6.12.1 Effets du transtypage¶

Le changement de type forcé (transtypage) entre des variables de différents types engendre des effets de bord qu'il faut connaître. Lors d'un changement de type vers un type dont le pouvoir de représentation est plus important, il n'y a pas de problème. À l'inverse, on peut rencontrer des erreurs sur la précision ou une modification radicale de la valeur représentée !

6.12.1.1 Transtypage d'un entier en réel¶

La conversion d'un entier (signé ou non) en réel (double ou float) n'a pas d'effet particulier. Le type

long l=3;
double d=(double)l; // valeur : 3 => OK

A l'exécution, la valeur de \(d\) sera la même que \(l\).

6.12.1.2 Transtypage d'un réel en entier¶

La conversion d'un nombre réel (double ou float) en entier (signé) doit être étudiée pour éviter tout problème. Le type entier doit être capable de recevoir la valeur (attention aux valeurs maxi).

double d=3.9;
long l=(long)d; // valeur : 3 => perte de précision

A l'exécution, la valeur de \(l\) sera la partie entière de \(d\). Il n'y a pas d'arrondi.

double d=0x12345678;
short sh=(short)d; // valeur : 0x5678 => changement de valeur

La variable sh (short sur 16 bit) ne peut contenir la valeur réelle. Lors du transtypage, il y a modification de la valeur ce qui conduit à des erreurs de calculs par la suite.

double d=-123;
unsigned short sh=(unsigned short)d; // valeur : 65413 => changement de valeur

L'utilisation d'un type non signé pour convertir un nombre réel conduit également à une modification de la valeur numérique.

6.12.1.3 Transtypage d'un double en float¶

La conversion d'un nombre réel de type double en réel de type float pose un problème de précision de calcul.

double d=0.1111111111111111;
float f=(float)d; // valeur : 0.1111111119389533 => perte de précision

À l'exécution, il y a une perte de précision lors de la conversion ce qui peut, lors d'un calcul itératif induire des erreurs de calcul.

Exercice 6.8¶

On considère les déclarations suivantes :

float x;
short i;
unsigned short j;
long k;
unsigned long l;

Identifiez les expressions ci-dessous dont le résultat n'est pas mathématiquement correct.

x = 1e6;
i = x;
j = -20;
k = x;
l = k;
k = -20;
l = k;

Exercice 6.9¶

Que valent les valeurs de p, x et n:

float x;
int n, p;

p = 2;
x = (float)15 / p;
n = x + 1.1;

Exercice 6.10¶

Soit les déclarations suivantes :

float x, y;
bool condition;

Réécrire l'expression ci-dessous en mettant des parenthèses montrant l'ordre des opérations :

condition = x >= 0 && x <= 20 && y > x || y == 50 && x == 2 || y == 60;

Donner la valeur de condition évaluée avec les valeurs suivantes de x et y:

x = -1.0; y = 60.;
x = 0; y = 1.;
x = 19.0; y = 1.0;
x = 0.0; y = 50.0;
x = 2.0; y = 50.0;
x = -10.0; y = 60.0;

Exercice 6.11¶

Vous participez à une revue de code et tombez sur quelques perles laissées par quelques collègues. Comment proposeriez-vous de corriger ces écritures ? Le code est écrit pour un modèle de donnée LLP64.

Pour chaque exemple, donner la valeur des variables après exécution du code.

```
unsigned short i = 32767;
i++;
```
```
short i = 32767;
i++;
```

short i = 0;
i = i--;
i = --i;
i = i--;

Exercice 6.12¶

Considérons les déclarations suivantes :

char c = 3;
short s = 7;
int i = 3;
long l = 4;
float f = 3.3;
double d = 7.7;

Que vaut le type et la valeur des expressions suivantes ?

c / 2
sh + c / 10
lg + i / 2.0
d + f
(int)d + f
(int)d + lg
c << 2
sh & 0xF0
sh && 0xF0
sh == i + lg
d + f == sh + lg

Exercice 6.13¶

Que vaut x?

float x = 10000000. + 0.1;

Exercice 6.14¶

Pour chaque entrée suivante, indiquez le nom et le type des variables que vous utiliseriez pour représenter les données dans ce programme :

Gestion d'un parking: nombre de voitures présente
Station météo
1. Température moyenne de la journée
2. Nombre de valeurs utilisées pour la moyenne
Montant disponible sur un compte en banque
Programme de calcul de d'énergie produite dans une centrale nucléaire
Programme de conversion décimal, hexadécimal, binaire
Produit scalaire de deux vecteurs plans
Nombre d'impulsions reçues par un capteur de position incrémental

Exercice 6.15¶

On considère un disque, divisé en 12 secteurs angulaires égaux, numérotés de 0 à 11. On mesure l’angle de rotation du disque en degrés, sous la forme d’un nombre entier non signé. Une flèche fixe désigne un secteur. Entre 0 et 29 °, le secteur désigné est le n° 0, entre 30 ° et 59 °, c’est le secteur 1, ...

Donnez une expression arithmétique permettant, en fonction d’un angle donné, d’indiquer quel est le secteur du disque se trouve devant la flèche. Note : l’angle de rotation peut être supérieur à 360 °. Vérifiez cette expression avec les angles de 0, 15, 29, 30, 59, 60, 360, 389, 390 degrés.

Écrivez un programme demandant l’angle et affichant le numéro de secteur correspondant.

Exercice 6.16¶

Il est prouvé mathématiquement que la somme des entiers strictement positifs pris dans l'ordre croissant peut être exprimée comme :

\[\sum_{k=1}^n k = \frac{n(n+1)}{2}\]

Un grand mathématicien Srinivasa Ramanujan (En tamoul: சீனிவாச இராமானுஜன்) à démontré que ce la somme à l'infini donne :

\[\sum_{k=1}^{\inf} k = -\frac{1}{12}\]

Vous ne le croyez pas et décider d'utiliser le superordinateur Pensées Profondes pour faire ce calcul. Comme vous n'avez pas accès à cet ordinateur pour l'instant (et probablement vos enfants n'auront pas accès à cet ordinateur non plus), écrivez un programme simple pour tester votre algorithme et prenant en paramètre la valeur n à laquelle s'arrêter.

Tester ensuite votre programme avec des valeurs de plus en plus grandes et analyser les performances avec le programme time:

$ time ./a.out 1000000000
500000000500000000

real    0m0.180s
user    0m0.172s
sys     0m0.016s

À partir de quelle valeur, le temps de calcul devient significativement palpable ?

Exercice 6.17¶

La société japonaise Nakainœil développe des systèmes de vision industriels pour l'inspection de pièces dans une ligne d'assemblage. Le programme du système de vision comporte les variables internes suivantes :

uint32_t inspected_parts, bad_parts;
float percentage_good_parts;

À un moment du programme, on peut lire :

percentage_good_parts = (inspected_parts - bad_parts) / inspected_parts;

Sachant que inspected_parts = 2000 et bad_parts = 200:

Quel résultat le développeur s'attend-il à obtenir ?
Qu'obtient-il en pratique ?
Pourquoi ?
Corrigez les éventuelles erreurs.

Exercice 6.18¶

Durant la guerre du Golfe le 25 février 1991, une batterie de missile américaine à Dharan en Arabie saoudite à échoué à intercepter un missile irakien Scud. Cet échec tua 28 soldats américains et en blessa 100 autres. L'erreur sera imputée à un problème de type de donnée sera longuement discutée dans le rapport GAO/OMTEC-92-26 du commandement général.

Un registre 24-bit est utilisé pour le stockage du temps écoulé depuis le démarrage du logiciel de contrôle indiquant le temps en dixième de secondes. Dès lors il a fallait multiplier ce temps par 1/10 pour obtenir le temps en seconde. La valeur 1/10 était tronquée à la 24:sup:ième décimale après la virgule. Des erreurs d'arrondi sont apparue menant à un décalage de près de 1 seconde après 100 heures de fonction. Or, cette erreur d'une seconde s'est traduite par 600 mètres d'erreur lors de la tentative d'interception.

Le stockage de la valeur 0.1 est donné par :

\[0.1_{10} \approx \lfloor 0.1_{10}\cdot 2^{23} \rfloor = 11001100110011001100_{2} \approx 0.09999990463256836\]

Un registre contient donc le nombre d'heures écoulées exprimées en dixième de seconde soit pour 100 heures :

\[100 \cdot 60 \cdot 60 \cdot 10 = 3'600'000\]

En termes de virgule fixe, la première valeur est exprimée en Q1.23 tandis que la seconde en Q0.24. Multiplier les deux valeurs entre elles donne Q1.23 x Q0.24 = Q1.47 le résultat est donc exprimé sur 48 bits. Il faut donc diviser le résultat du calcul par \(2^{47}\) pour obtenir le nombre de secondes écoulées depuis le début la mise sous tension du système.

Quel est l'erreur en seconde cumulée sur les 100 heures de fonctionnement ?